Swin Transformer V2

Introduction

该论文目的是解决如下问题：

  1. 训练时的不稳定性。
  2. 如何有效将低像素预训练的模型迁移到更高的像素上。

提出的解决方式：

  • 残差后归一化技术。
  • 缩放余弦注意力方法可提高大视觉模型的稳定性。
  • 对数间隔连续位置偏差技术。

Study on bias terms： 在 NLP 中，相对位置偏置法被证明是有益的，而不是原始 Transformer 中使用的绝对位置嵌入法。在计算机视觉中，相对位置偏置法更常用，这可能是因为视觉信号的空间关系在视觉建模中起着更重要的作用。常见的做法是直接学习偏置值作为模型权重。也有一些作品特别研究了如何设置和学习偏置项。

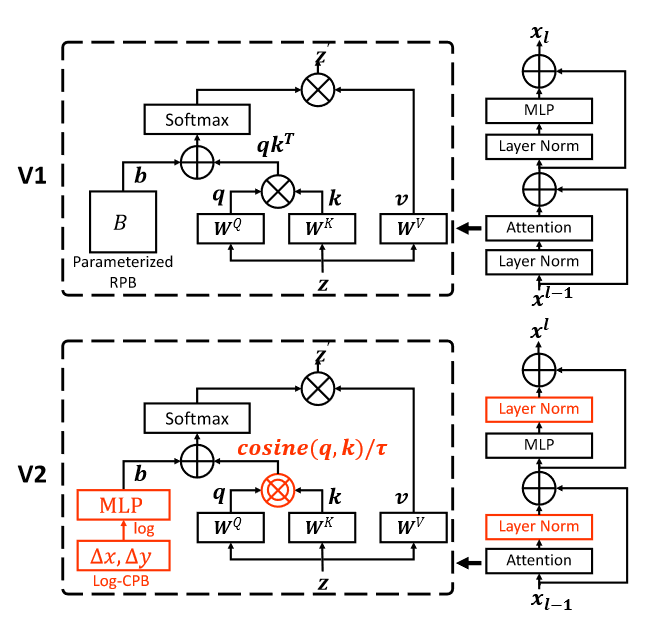
​ Figure 1：Swin Transformer V1与V2结构对比

模型

Relative position bias

$$
Attention(Q,K,V)=SoftMax(QK^T/ \sqrt{d} + B )V
$$

  • $B\in{R}^{M^2×M^2}$

  • $M^2$是一个window中patch的数量。

  • $Q,K,V\in{R^{M^2×d}}$ 是query，key和value。

  • d是隐藏层维度

在 Swin Transformer 中，沿每个轴的相对位置在 [−M + 1, M − 1] 范围内

相对位置偏差被参数化为偏差矩阵$\hat B∈R(2M−1)×(2M−1) $ B中元素取自$\hat B$

源码：

1
2
3
4
5
6
#torch.arange默认的步长为1
relative_coords_h = torch.arange(-(self.window_size[0] - 1), self.window_size[0], dtype=torch.float32)
relative_coords_w = torch.arange(-(self.window_size[1] - 1), self.window_size[1], dtype=torch.float32)
relative_coords_table = torch.stack(
     torch.meshgrid([relative_coords_h,
                    relative_coords_w])).permute(1, 2, 0).contiguous().unsqueeze(0)  # 1,2*Wh-1,2*Ww-1,2

经这个函数形成如下格式的4维矩阵
$$
R^{1×(2Wh-1)×(2Ww-1)×2}
$$
解析：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import torch
relative_coords_h = torch.arange(-(5 - 1), 5, dtype=torch.float32)
relative_coords_w = torch.arange(-(4 - 1), 4, dtype=torch.float32)

print(relative_coords_h)
print(relative_coords_w)
tensor([-4., -3., -2., -1.,  0.,  1.,  2.,  3.,  4.])
tensor([-3., -2., -1.,  0.,  1.,  2.,  3.])

# torch.meshgrid()函数创建两个张量的网格坐标。relative_coords_h和relative_coords_w分别是两个一维张量，表示高度方向和宽度方向的相对坐标。这个函数返回两个张量，分别表示高度方向和宽度方向上的网格坐标。
t = torch.meshgrid([relative_coords_h,relative_coords_w])

(tensor([[-4., -4., -4., -4., -4., -4., -4.],
         [-3., -3., -3., -3., -3., -3., -3.],
         [-2., -2., -2., -2., -2., -2., -2.],
         [-1., -1., -1., -1., -1., -1., -1.],
         [ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
         [ 1.,  1.,  1.,  1.,  1.,  1.,  1.],
         [ 2.,  2.,  2.,  2.,  2.,  2.,  2.],
         [ 3.,  3.,  3.,  3.,  3.,  3.,  3.],
         [ 4.,  4.,  4.,  4.,  4.,  4.,  4.]]),
 tensor([[-3., -2., -1.,  0.,  1.,  2.,  3.],
         [-3., -2., -1.,  0.,  1.,  2.,  3.],
         [-3., -2., -1.,  0.,  1.,  2.,  3.],
         [-3., -2., -1.,  0.,  1.,  2.,  3.],
         [-3., -2., -1.,  0.,  1.,  2.,  3.],
         [-3., -2., -1.,  0.,  1.,  2.,  3.],
         [-3., -2., -1.,  0.,  1.,  2.,  3.],
         [-3., -2., -1.,  0.,  1.,  2.,  3.],
         [-3., -2., -1.,  0.,  1.,  2.,  3.]]))
# torch.stack的作用就是将上面的两个二维矩阵合并成一个三维矩阵
t = torch.stack(t)
t.shape
torch.Size([2, 9, 7])

# permute(1,2,0)函数将该三维矩阵进行变形
tensor([[[-4., -3.],
         [-4., -2.],
         [-4., -1.],
         [-4.,  0.],
         [-4.,  1.],
         [-4.,  2.],
         [-4.,  3.]],
...
         [ 4., -1.],
         [ 4.,  0.],
         [ 4.,  1.],
         [ 4.,  2.],
         [ 4.,  3.]]])

# contiguous()：将张量在内存中变为连续存储，确保后续操作的正确性。
# unsqueeze(0)：在第0维度上增加一个维度，将三维张量变为四维张量。这样做是为了与后续操作的张量形状相匹配。
1

Continuous relative position bias

$$
B(\Delta x,\Delta y)=G(\Delta x,\Delta y)
$$
G是一个小型网络，中间使用ReLU激活的两层MLP。

元网络 G 为任意相对坐标生成偏差值，因此可以自然地转移到具有任意变化窗口大小的微调任务。在推论中，可以预先计算每个相对位置的偏差值并将其存储为模型参数，使得推论与原始参数化偏差方法相同。

Log-spaced coordinates

通过使用对数间隔坐标，当我们在窗口分辨率上传递相对位置偏差时，所需的外推率将比使用原始线性间隔坐标小得多。对于从预训练的 8 × 8 窗口大小转移到微调的 16 × 16 窗口大小的示例，使用原始原始坐标，输入坐标范围将从 [−7, 7]×[−7，7]至[−15, 15]×[−15, 15]。外推比为原始范围的 8/7 = 1.14倍。使用对数间隔坐标，输入范围将从 [−2.079, 2.079] × [−2.079, 2.079] 到 [−2.773, 2.773] × [−2.773, 2.773]。

这篇文章的外推比意思是值的大小差除以原始值：
$$
8=15-7\
Extrapolation Ratio = 8/7 \
\Delta = 2.773-2.079 = 0.684\
Extrapolation Ratio = \frac{0.684}{2.079} = 0.333
$$

  • 源码
1
2
3
4
5
6
7
8
9
if pretrained_window_size[0] > 0:
    relative_coords_table[:, :, :, 0] /= (pretrained_window_size[0] - 1)
    relative_coords_table[:, :, :, 1] /= (pretrained_window_size[1] - 1)
else:
    relative_coords_table[:, :, :, 0] /= (self.window_size[0] - 1)
    relative_coords_table[:, :, :, 1] /= (self.window_size[1] - 1)
relative_coords_table *= 8  # normalize to -8, 8
relative_coords_table = torch.sign(relative_coords_table) * torch.log2(
           torch.abs(relative_coords_table) + 1.0) / np.log2(8)
  • 公式

$$
\hat{\Delta x} = sign(x)*log(1+|{\Delta x}|),\
\hat{\Delta y} = sign(y)*log(1+|{\Delta y}|)
$$

Scaled cosine attention

原始的自注意力计算，相似的像素对是使用点积来计算query和key向量的。当这种方法被用到大的视觉模型上时一些块和头的学习注意力图经常由几个像素对主导，特别是在 res-post-norm 配置中。
$$
Sim(q_i,k_j)=\cos(q_i,k_i)/τ +B_{ij}
$$
​ $\tau$ 是一个可学习参数

经过查阅源码发现其本质就是在点积前进行归一化保证最后进行点积的向量的长度是单位长度，最后出来的点积结果就是两向量间的角度。

  • 源码：
1
2
3
attn = (F.normalize(q, dim=-1) @ F.normalize(k, dim=-1).transpose(-2, -1))
logit_scale = torch.clamp(self.logit_scale, max=torch.log(torch.tensor(1. / 0.01))).exp()
attn = attn * logit_scale
  • 解析
  1. attn = (F.normalize(q, dim=-1) @ F.normalize(k, dim=-1).transpose(-2, -1))
    这行代码计算了查询（q）和键（k）之间的注意力得分。首先，通过 F.normalize 函数对查询和键进行归一化，使它们具有单位长度。然后，使用矩阵乘法 @ 计算查询和键的内积，得到注意力得分矩阵 attn。这个矩阵描述了查询与每个键的相关性或相似度。
  2. logit_scale = torch.clamp(self.logit_scale, max=torch.log(torch.tensor(1. / 0.01))).exp()
    这行代码通过对 self.logit_scale 进行限制和指数化，得到一个用于缩放注意力得分的比例因子。self.logit_scale 可能是一个模型参数，通过对其进行限制，确保缩放因子不会过大。torch.clamp 函数用于限制 self.logit_scale 的最大值为 torch.log(torch.tensor(1. / 0.01))，然后使用 exp() 函数进行指数化。
  3. attn = attn * logit_scale
    这行代码将注意力得分矩阵 attn 与缩放因子 logit_scale 相乘，对注意力得分进行缩放。这个缩放操作可以调整注意力权重的范围和重要性，以适应模型的需要。

后置归一化

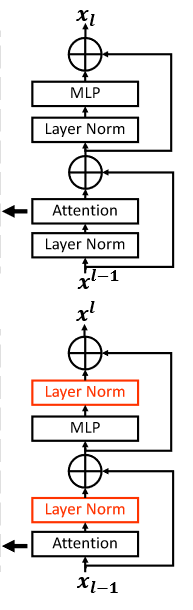
  • 原先问题

如上图所示，原先的前置归一化手段会使得每次合并后幅度被积累（因为先进行归一化再进行Attention的，也就是Attention这一步可能会将输出值变得幅度很大（因为有投影））

  • 改进后

在这种方法中，每个残差块的输出在合并回主分支之前被归一化，并且当层更深时主分支的幅度不会累积。