GELU

研究者表明，收到dropout、ReLU等机制的影响，它们都希望将不重要的激活信息规整为0，我们可以理解为，对于输入的值，我们根据它的情况乘上1或者0，更数学一点的描述是，对于每一个输入x，其服从标准的正太分布 N(0,1) ,它会乘上一个伯努利分布 $Bernoulli(\phi(x))$ 其中，$\phi(x)=P(X<x)$ 。

随着x的降低，它被归零的概率会升高，对于ReLU来说，这个界限就是0，输入少于零就会被归为0，这一类激活函数，不仅保留了概率性，同时也保留了对输入的依赖性。

GELU ：高斯误差线性单元激活函数，在最近的Transformer模型（谷歌的BERT和OpenAI的GPT-2）中得到了应用,GELU的论文来自2016年，但是最近才引起关注，这种激活函数的形式为：
$$
xP(X<x)=x\phi(x)
$$
其中$\phi(x)$ 是高斯正态分布的累积分布：
$$
xP(X<x) = x \int^x_{-\infty}\frac{e^{-\frac{(x-\mu)^2}{2\sigma^2}}}{\sigma \sqrt{2\pi}} dX
$$
其约等于：
$$
GELU(X)=0.5x(1+tanh(\sqrt{2/\pi}(x+0.044715x^3)))
$$

正态分布

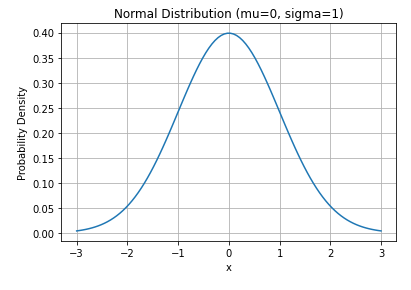
首先展示一下正态分布的函数：
$$
f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}
$$
下面画一下N(0,1)的图像：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

def plot_normal(mu, sigma):
    x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)  # 生成一系列x值
    y = norm.pdf(x, mu, sigma)  # 计算对应x值的正态分布概率密度函数值

    plt.plot(x, y)  # 绘制正态分布曲线
    plt.xlabel('x')
    plt.ylabel('Probability Density')
    plt.title('Normal Distribution (mu={}, sigma={})'.format(mu, sigma))
    plt.grid(True)
    plt.show()

# 设置正态分布的均值和标准差
mu = 0
sigma = 1

# 绘制正态分布的PDF图
plot_normal(mu, sigma)

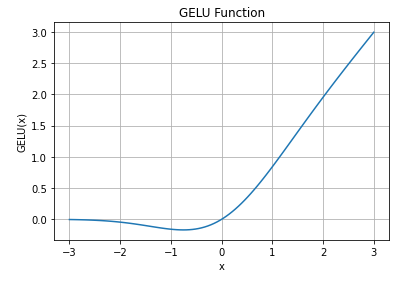
GELU图像

GELU函数图像：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np
import matplotlib.pyplot as plt

def gelu(x):
    return 0.5 * x * (1 + np.tanh(np.sqrt(2/np.pi) * (x + 0.044715 * x**3)))

# 生成x的取值范围
x = np.linspace(-3, 3, 100)

# 计算对应的y值
y = gelu(x)

# 绘制函数图像
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('GELU(x)')
plt.title('GELU Function')
plt.grid(True)
plt.show()

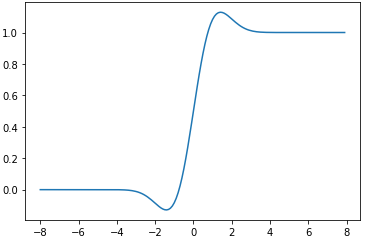
GELU函数导数图像：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import numpy as np
import matplotlib.pyplot as plt
import torch
def gelu_1(x):
    #使用numpy实现
    return 0.5*x*(1 + np.tanh(np.sqrt(2/np.pi)*(x + 0.044715*x**3)))

def gelu_dao(inputs):
    return ((np.tanh((np.sqrt(2) * (0.044715 * inputs ** 3 + inputs)) / np.sqrt(np.pi)) + ((np.sqrt(2) * inputs * (
                0.134145 * inputs ** 2 + 1) * ((1 / np.cosh(
        (np.sqrt(2) * (0.044715 * inputs ** 3 + inputs)) / np.sqrt(np.pi))) ** 2)) / np.sqrt(np.pi) + 1))) / 2

def plot_gelu():
    x1=np.arange(-8,8,0.1)
    y1=gelu_1(x1)
    #plt.plot(x1,y1)
    y2=gelu_dao(x1)
    
    plt.plot(x1,y2)
    plt.show()

if __name__ == '__main__':
    plot_gelu()