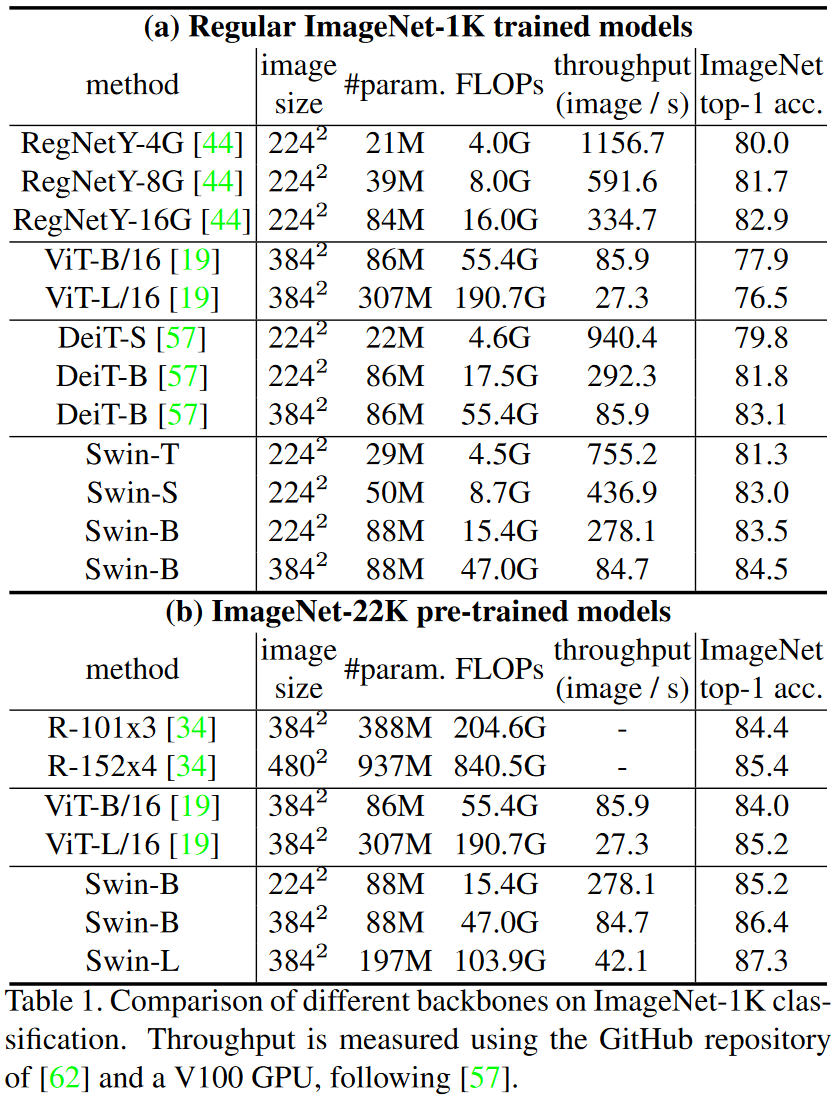
Swin Transformer

introduction

本文目标就是寻求扩展 Transformer 的适用性，使其可以作为计算机视觉的通用骨干，就像它在 NLP 中的作用以及 CNN 在视觉中的作用一样。

挑战

将Transformer在语言领域的高性能转移到视觉领域的重大挑战可以通过两种模式之间的差异来解释。

  1. 规模。与作为语言 Transformer 中处理的基本元素的单词标记不同，视觉元素在规模上可能存在很大差异，这一问题在对象检测等任务中受到关注。在现有的基于 Transformer 的模型中，令牌都是固定规模的，这种属性不适合这些视觉应用。
  2. 图像中像素的分辨率比文本段落中的单词要高得多。存在许多视觉任务，例如语义分割，需要在像素级进行密集预测，这对于高分辨率图像上的 Transformer 来说是很棘手的，因为其自注意力的计算复杂度与图像大小成二次方。

为了克服这些问题，本文提出了一个通用的 Transformer 主干，称为 Swin Transformer，它构建分层特征图，并且具有与图像大小线性的计算复杂度。如图 1(a) 所示，Swin Transformer 通过从小尺寸补丁（灰色轮廓）开始并逐渐合并更深 Transformer 层中的相邻补丁来构建分层表示。借助这些分层特征图，Swin Transformer 模型可以方便地利用先进技术进行密集预测，线性计算复杂度是通过在分割图像的非重叠窗口（以红色框出）内本地计算自注意力来实现的。每个窗口中的补丁数量是固定的，因此复杂度与图像大小成线性关系。这些优点使 Swin Transformer 适合作为各种视觉任务的通用骨干网，与之前基于 Transformer 的架构形成鲜明对比，后者生成单一分辨率的特征图并具有二次复杂度。

解决方式

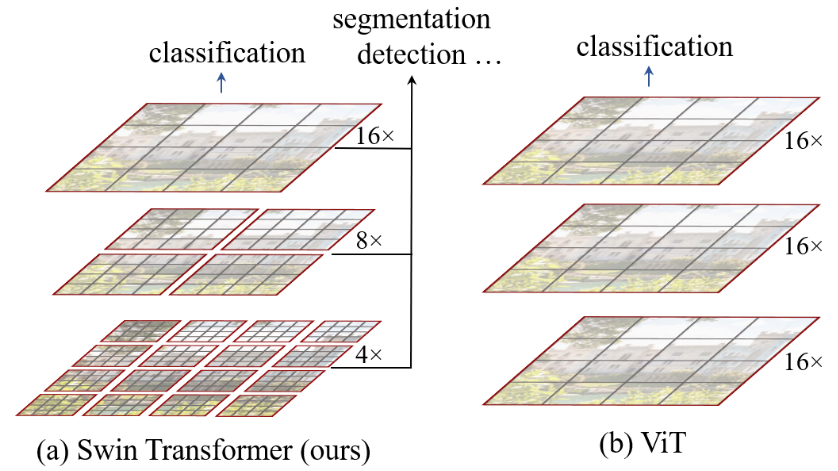
​ 图1

所提出的 Swin Transformer 通过合并更深层中的图像块（以灰色显示）来构建分层特征图，并且由于仅在每个局部窗口（以红色显示）内计算自注意力，因此具有输入图像大小的线性计算复杂性。因此，它可以作为图像分类和密集识别任务的通用主干。 (b) 相比之下，之前的视觉 Transformers 产生单个低分辨率的特征图，并且由于全局自注意力的计算，输入图像大小的计算复杂度为二次方

结构

移位窗口的实现形式

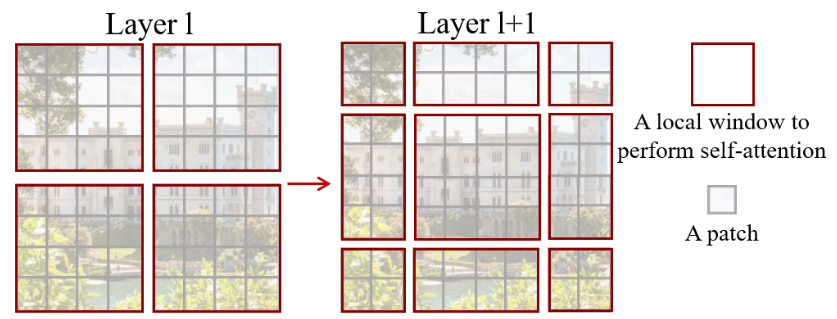
在 l 层（左）中，采用常规窗口划分方案，并在每个窗口内计算自注意力。在下一层 l + 1（右）中，窗口分区发生移动，产生新的窗口。新窗口中的自注意力计算跨越了 l 层中先前窗口的边界，提供了它们之间的连接。

首先通过补丁分割模块（如 ViT）将输入 RGB 图像分割成不重叠的补丁。每个补丁都被视为一个“令牌”，其特征被设置为原始像素 RGB 值的串联。在我们的实现中，我们使用 4 × 4 的块大小，因此每个块的特征维度为 4 × 4 × 3 = 48。线性嵌入层应用于此原始值特征，将其投影到任意维度（记为C)。

  1. 阶段1：

    在这些补丁标记上应用几个经过修改的自注意计算变换器块（Swin 变换器块）。变换器块保持标记的数量（$\frac{H}{4}\frac{W}{4}$）（原因是我们第一层的patch是44大小），并进行线性嵌入。

  2. 阶段2：

    为了产生分层表示，随着网络的深入，会通过补丁合并层来减少标记的数量。第一个补丁合并层将每组 2 × 2 相邻补丁的特征串联起来，并在 4C 维串联特征上应用线性层。（每个patch原先是$44$大小经过拉直和线性投影变成$1C$的大小，而这一层经过结合4个patch形成$4C$的维度（拉直））
    $$
    \begin{bmatrix}
    a & b \
    c & d \
    \end{bmatrix}
    $$
    a，b，c，d分别代表相邻的2    2的patch。由于经过flatten和投影，他们中每一个其实是$a,b,c,d\in R^{1×C}$ 的矩阵。

    将他们合并形成 $R^{4×C}$ 再将其拉直就变成了4*C的维度串。

    这就将标记数减少了 2 × 2 = 4 的倍数（分辨率降低了 2 倍），输出维度设置为 2C。随后应用 Swin 变换器块进行特征变换，分辨率保持为 $\frac{H}{4}*\frac{W}{4}$。这第一块补丁合并和特征变换被称为 “阶段 2”。

    下图中阶段1到阶段2之所以会变成$\frac{H}{8}*\frac{W}{8}$ 因为一次取4个相邻的patch相较于原先就是横纵各少了两倍。

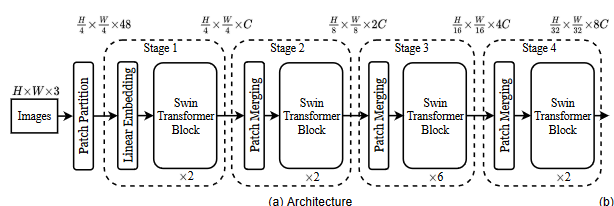
该过程重复两次，即“阶段 3”和“阶段 4”，输出分辨率分别为 $\frac{H}{16}*\frac{W}{16}$和 $\frac{H}{32}*\frac{W}{32}$。这些阶段共同产生层次表示，具有与典型卷积网络相同的特征图分辨率。因此，所提出的架构可以方便地替换现有方法中用于各种视觉任务的主干网络。

Swin Transformer block

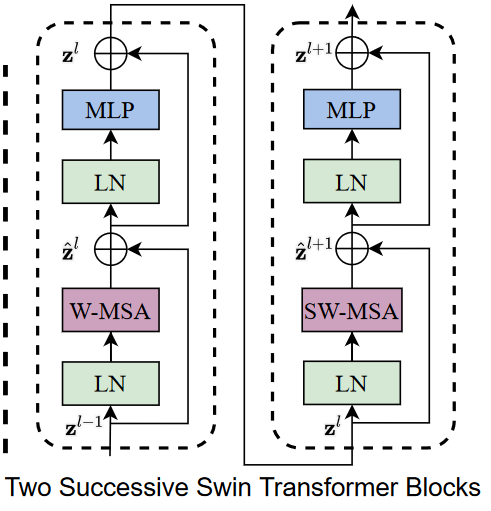
Swin Transformer 模块 Swin Transformer 是通过将 Transformer 模块中的标准多头自注意力（MSA）模块替换为基于移位窗口的模块而构建的，其他层保持不变。Swin Transformer 模块由基于移位窗口的 MSA 模块组成，后跟中间带有 GELU 非线性的 2 层 MLP。在每个 MSA 模块和每个 MLP 之前应用 LayerNorm (LN) 层，并在每个模块之后应用残差连接。

  1. 计算复杂度对比

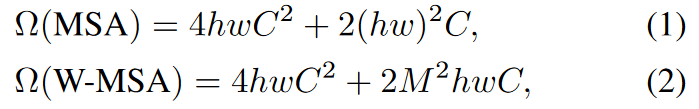
假设每个窗口包含 M × M 个补丁，则全局 MSA 模块和基于 h × w 补丁图像的窗口的计算复杂度为上图所示。

推导过程：

  • MSA：一个自注意力模块其实就是4个投影和中间的2个内积。

    • 投影：

      假设每个补丁大小为 r*r，那么将其拉直后整个图片变成 $R^{(h×w)×(r×r)}$ 经过前置投影变成 $R^{(h×w)×C}$

      将该矩阵传入MSA模块后，投影复杂度应为如下表示：
      $$
      R^{(h×w)×C} → R^{(h×w)×C}输入经过一个R^{C×C}的矩阵
      $$
      复杂度就是如下表示
      $$
      \sum^4_{i=1}h×w×C×C
      $$

    • 内积：

    $R^{(h×w)×C}$与$R^{(h×w)×C}$内积的复杂度如下
    $$
    \sum^{2}_{i=1}h×w×C×h×w
    $$

  • W-MSA：

    • 投影复杂度与MSA一致
    • 内积

    图片被分为$\frac{h×w}{M×M}$个窗口，每个窗口展开是$R^{(M×M)×C}$ 的矩阵那么复杂度计算为下式
    $$
    \sum^{\frac{h×w}{M×M}}{i=1} \sum{i1=1}^2 M×M×C×M×M
    $$

  1. 移动划分方式

第一个模块使用从左上角像素开始的常规窗口划分策略，将 8 × 8 特征图均匀划分为大小为 4 × 4 (M = 4) 的 2 × 2 窗口。然后，下一个模块采用与前一层的窗口配置不同的窗口配置，通过将窗口从规则分区的窗口中移动（$\frac{M}{2}$，$ \frac{M}{2}$）个像素。(可以理解为上移再右移)

使用移位窗口分区方法，连续的 Swin Transformer 块计算如下

其中 $z^{l’}$ 和 zl 分别表示块 l 的 (S)WMSA 模块和 MLP 模块的输出特征, W-MSA 和 SW-MSA 分别表示使用常规和移位窗口分区配置的基于窗口的多头自注意力。

  • 移位配置的高效批量计算移位窗口分区的一个问题是，它将导致更多的窗口，从移位配置中的 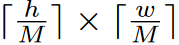到

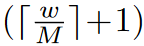    ，并且一些窗口将小于 M × M 。一个简单的解决方案是将较小的窗口填充到 M × M 的大小，并在计算注意力时屏蔽掉填充的值。当常规分区中的窗口数量较少时，例如2 × 2，这种朴素解决方案增加的计算量是相当可观的（2 × 2 → 3 × 3，增加了 2.25 倍）。在这里，我们提出了一种更有效的批量计算方法，通过向左上方向循环移位，如图 4 所示。经过这种移位，批处理窗口可能由多个在特征图中不相邻的子窗口组成，因此采用屏蔽机制将自注意力计算限制在每个子窗口内。通过循环移位，批处理窗口的数量保持与常规窗口划分相同，因此也是高效的。该方法的低延迟如表所示

训练

设置

  1. 优化器: 使用 AdamW优化器进行 300 个周期，使用余弦衰减学习率调度器和 20 个周期的线性预热。使用的批量大小为 1024，初始学习率为 0.001，权重衰减为 0.05。

训练中包含了[57]的大多数增强和正则化策略，除了重复增强[28]和EMA[41]，它们不会提高性能。请注意，这与[57]相反，其中重复增强对于稳定 ViT 训练至关重要。

[57]Hugo Touvron, Matthieu Cord, Matthijs Douze, Francisco Massa, Alexandre Sablayrolles, and Herv ́ e J ́ egou. Training data-efficient image transformers & distillation through attention. arXiv preprint arXiv:2012.12877, 2020.

[28] Elad Hoffer, Tal Ben-Nun, Itay Hubara, Niv Giladi, Torsten Hoefler, and Daniel Soudry. Augment your batch: Improving generalization through instance repetition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 8129–8138, 2020. 6

[41] Boris T Polyak and Anatoli B Juditsky. Acceleration of stochastic approximation by averaging. SIAM journal on control and optimization, 30(4):838–855, 1992.

实验