ViT
整体思路
- 将图片分成多个patch(16*16)
- 将每个patch进行投影作为类似NLP领域中的token
- 再将这些‘token’传入标准transformer网络中。
在中小型数据集上训练出来的效果不佳,但是当训练集的规模增大时收获了极好的结果。
Related work
- 最原始的想法是将图片的每个像素都关注其他的每个像素。但这样做的成本是像素点数目的二次方,显然不适用于现实输入尺寸。
- 对于自注意力机制,假设有n个像素点。每个像素点都会对n个像素进行注意力机制。
$$
\sum_{i=1}^n1*n=n^2
$$
- 只在查询像素的局部邻域内引入自注意力机制而不是全局
- 使用2*2的网格去分割图像,但是这样做的后果是仅适用于小分辨率图像。
- 将CNN与各种形式的自注意力机制结合
模型结构
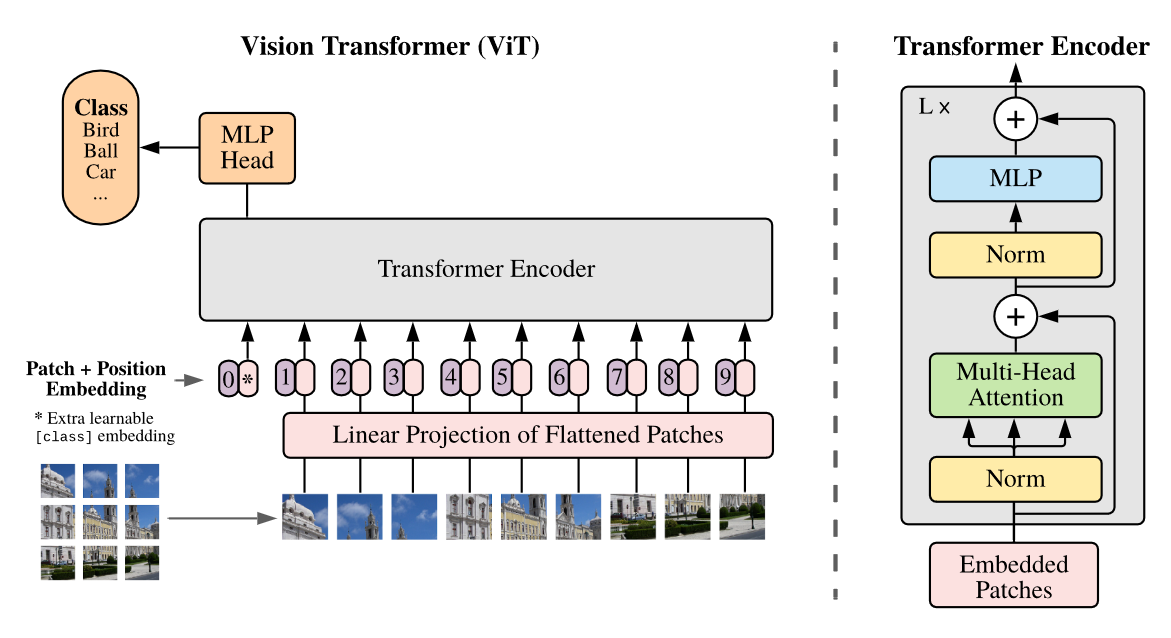
我们将图像分割成固定大小的片段,对每个片段进行线性嵌入,添加位置嵌入,然后将得到的向量序列输入标准变换器编码器。为了进行分类,我们采用标准方法,在序列中添加额外的可学习 “分类标记”。

模型输入
给定输入图像 $x\in R^{HWC}$ 将其处理为$x_p \in R^{N*(P^2C)}$
(P, P) :是每个图像补丁的分辨率
N:$(HWC)/(P^2C)=HW/P^2$ ,就是生成的patch数,也是transformer的有效输入序列长度
(H, W) :是原始图像的分辨率
C:通道数
transformer的隐藏层向量大小D,因此我们使用可训练的线性投影将patch进行flatten并映射到D维(公式1)。我们将该投影的输出称为补丁嵌入。
与BERT 的 [class] 标记类似,我们在嵌入补丁序列前面添加一个可学习的嵌入($z^0_0=x_{class}$ ) ,其 Transformer 编码器 ($z^0_L$) 输出处的状态用作图像表示 y(公式4)。在预训练和微调期间,分类头都附加到 z0 L。分类头在预训练时由具有一个隐藏层的 MLP 实现,在微调时由单个线性层实现。
位置嵌入$E_{pos}$被添加到补丁嵌入中以保留位置信息。我们使用标准的可学习 1D 位置嵌入。
混合结构
作为原始图像补丁的替代方案,输入序列可以由 CNN 的特征图形成。在这种混合模型中,补丁嵌入投影 E(公式 1)应用于从 CNN 特征图中提取的补丁。作为一种特例,补丁的空间尺寸可以是 1x1,这意味着输入序列可以通过简单地平铺特征图的空间维度并投影到变换器维度来获得。分类输入嵌入和位置嵌入如上所述。
公式
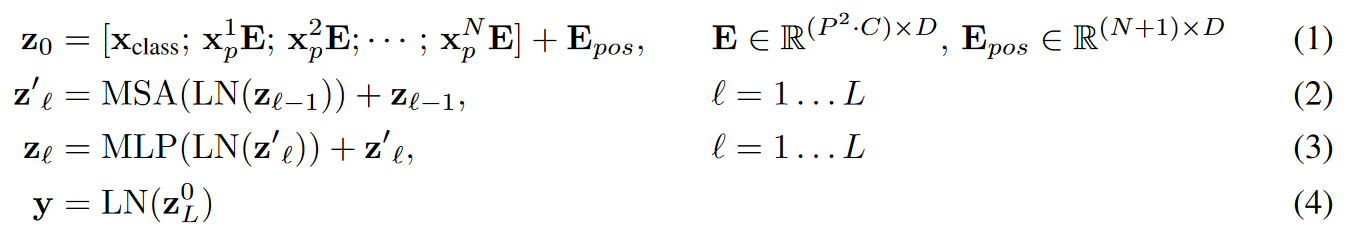
公式2的MSA是multiheaded self-attention。
LN是Layernorm
MLP 包含两个具有 GELU 非线性的层。
微调
在大型数据集上对 ViT 进行预训练,然后根据(较小的)下游任务进行微调。
在微调时移除预训练的预测头,并附加一个零初始化的 D × K 前馈层,其中 K 是下游类别的数量。与预训练相比,在更高分辨率下进行微调通常是有益的。当输入更高分辨率的图像时,我们会保持补丁大小不变,这样就会增加有效序列长度。视觉转换器可以处理任意长度的序列(受内存限制),但是,预训练的位置嵌入可能不再有意义。因此,我们根据预训练位置嵌入在原始图像中的位置,对其进行二维插值。需要注意的是,只有在调整分辨率和提取补丁时,才会手动向视觉转换器注入有关图像二维结构的归纳偏差。
使用 Adam 训练包括 ResNets 在内的所有模型,β1 = 0.9,β2 = 0.999,批量大小为 4096,并应用 0.1 的高权重衰减,(Adam 对 ResNets 的效果略好于 SGD)。我们使用线性学习率预热和衰减,
为了进行微调,我们对所有模型都使用了带动量的 SGD,批量大小为 512,。对于表 2 中的 ImageNet 结果,我们使用了更高的分辨率进行微调:对于表 2 中的 ImageNet 结果,我们使用了更高的分辨率进行微调:ViT-L/16 为 512 分辨率,ViT-H/14 为 518 分辨率,同时还使用了 Polyak & Juditsky(1992 年)的平均值,系数为 0.9999。
测验

右图:用于测试ViT的图像信息整合能力(注意力权重计算图像空间中信息整合的平均距离。这种“注意力距离”类似于 CNN 中的感受野大小)。可以发现即使是第0层的attention也有head注意到了大部分图像,其他的head在低层的注意力距离始终较小(局部注意),随着层深度增加注意力距离也在不断增加。
中间:模型学会在位置嵌入的相似性中对图像内的距离进行编码,距离较近的斑块往往具有更相似的位置嵌入。此外,还出现了行列结构;同一行/列中的补丁具有相似的嵌入。(用于研究位置编码)
这个可能是如下的理解:
假如一张图片被分为4个patch,
$$
\begin{bmatrix}
X_1 & X_2 \
X_3 & X_4 \
\end{bmatrix}
$$
每个patch进行拉直之类的操作,那么每一行就是一个$R^{2n}$的矩阵,每一列也同理,因此对于上图每一个小格就变成了一个$R^{22}$的矩阵,(1,1)代表X1与自己,(1,2)代表X1与X3的相似度,而出现暗淡的(2,2)其实就是X2与X3的相似度。
左图:展示了对于投影层的主成分分析,可以看到有一些纹理和颜色的特征。ViT-L/32 的 RGB 值的初始线性嵌入的滤波器。