上采样(UpSampling)与下采样(DownSampling)

缩小图像（称为下采样或降采样）的主要目的有两个：

使得图像符合显示区域的大小；
生成对应图像的缩略图。

放大图像（或称为上采样或图像插值）的主要目的是：放大原图像,从而可以显示在更高分辨率的显示设备上。

上采样和下采样都是一种抽象描述，其具体实现有很多种方式：

下采样：

用stride为2的卷积层实现：卷积过程导致的图像变小是为了提取特征。下采样的过程是一个信息损失的过程，而池化层是不可学习的，用stride为2的可学习卷积层来代替pooling可以得到更好的效果，当然同时也增加了一定的计算量。
用stride为2的池化层实现：池化下采样是为了降低特征的维度。如Max-pooling和Average-pooling，目前通常使用Max-pooling，因为他计算简单而且能够更好的保留纹理特征。

==下采样就是卷积或者池化过程。==

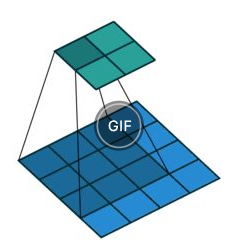
使用矩阵计算卷积

还是上面那个具体的例子，将输入的矩阵 ( 4×4 )展开变成一个16维的列向量，得到

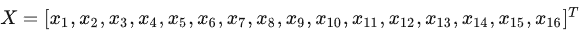
输出的图像展开为4维的列向量

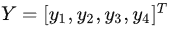
将卷积核展开，变成 4×16 的稀疏矩阵，其形式为Toeplitz 矩阵，4是对应输出的维数

（Toeplitz 矩阵，即每一行中的元素都与上一行的对应位置平移一个单位的元素相同）

卷积运算则 Y=CX

上面的结果得到的 Y是一个 4维的列向量，再将其reshape成 2×2 ，则得到输出的图像。

通过矩阵乘法，我们则可以得到反卷积 X=C^T^Y

上采样：

上采样有3种常见的方法：双线性插值(bilinear)，反卷积(Transposed Convolution)，反池化(Unpooling)

插值：最近邻插值、双线性插值、双三次插值，效果和计算量逐个上升；虽然插值式上采样已没人用，但是下采样过程（数据准备从HRGT到LR）最常用的还是双三次。
基于插值的上采样方法只能通过图像的本身内容提高图像的分辨率，并没有带来更多信息，相反还有噪声放大、计算复杂度增加、结果模糊等副作用。
转置卷积又或是说反卷积(Transpose Conv)，通过对输入feature map间隔填充0，再进行标准的卷积计算，可以使得输出feature map的尺寸比输入更大；相比上池化，使用反卷积进行图像的“上采样”是可以被学习的（会用到卷积操作，其参数是可学习的）。

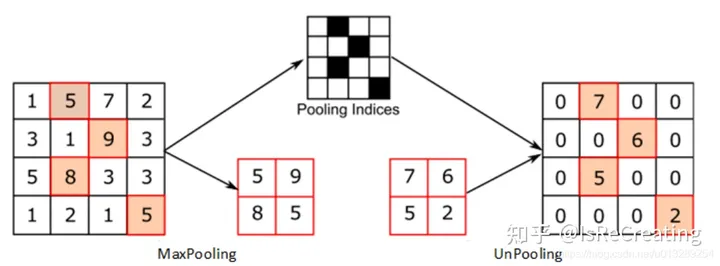
Up-Pooling - Max Unpooling && Avg Unpooling –Max Unpooling，在对称的max pooling位置记录最大值的索引位置，然后在unpooling阶段时将对应的值放置到原先最大值位置，其余位置补0；

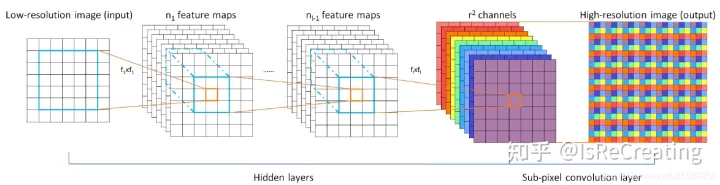
PixelShuffle（像素重组）

反卷积
- 由于卷积核一般比原始图像小，所以卷积之后的图像尺寸往往会变小。有时候我们需要将卷积后的图像还原成原始图像的尺寸，即实现图像从小分辨率到大分辨率的映射，这种操作就叫做上采样（Upsampling）。而反卷积正是一种上采样方法。
  
  反卷积，又称为转置卷积（Transposed Convolution,），它是一种特殊的卷积，先padding来扩大图像尺寸，紧接着跟正向卷积一样，旋转卷积核180度，再进行卷积计算。看上去就像，已知正向卷积的输出图像，卷积核，得到正向卷积中的原始图像（并非真的得到原始图像，像素点是不一样的，但是尺寸是一致的）。
  
  它看上去像是正向卷积的逆运算，但其实并不是。因为反卷积只能还原原始图像的尺寸，但是并不能真的恢复原始图像内容，即每个元素值其实是不一样的。
  
  卷积过程中：
  
  o 表示输出， i 表示输入， k :表示kernel的大小， p：表示padding, s : 表达strides
  
  反卷积过程中：
  
  o′ 表示输出， i′ 表示输入， k′ :表示kernel的大小， p′：表示padding, s′ : 表达strides
  
  卷积后的 o 则反卷积的 i′ , 一般卷积核是不会变的， k=k′ ，需要注意的是，卷积与反卷积的padding很可能是不一样。
  
  2.1 Striding
  
  反卷积的Striding跟卷积有点不一样，它在输入的每个元素之间插入 �′−1 个值为0的元素

如果我们将反卷积看成是一种特殊的卷积，它其实是根据反卷积中指定的步长strides, 修改了输入 i′, 根据strding 进行补0操作，得到 Is , 其大小变为 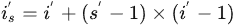, 然后对 Is 进行s=1的卷积。例如，对应上面的三个子图， s′=1 对应的 is′=3 , s′=2 对应的 is′=5 ， s′=3 对应的 is′=7 。